Repeal Ohm’s Law!

A Quantitative Path for Resistance

The Galvanometer

In 1820, Hans Christian Oersted and Andre-Marie Ampere discovered that a current passing through a wire would torque compass needle in a direction that is at a right angle to the direction of the current, and that discovery led to the creation of the uncalibrated tangent galvanometer.^[1]^[2] These devices use a current to displace a magnetized needle in the presence of Earth’s magnetic field. Unfortunately, each of these instruments had an unknown calibration constant due to the variability and orientation of the Earth’s magnetic field near the test location.

A Constant Potential Difference Source

Two years later, Thomas Seebeck discovered that two dissimilar metals with junctions held at two different temperatures would cause a deflection in a compass needle held near a wire. Seebeck attributed it to magnetism, but other scientists at the time believed it generated a voltage.^[3] This thermoelectric-effect reliably produced a repeatable constant potential difference source that voltaic piles of the time could not.

Thomas Seebeck discovered that he could generate an electromotive force by placing the connections of dissimilar metals in different temperature baths. Today, we call this the thermoelectric effect.

In 1825, a half-century after Cavendish performed his unknown and rudimentary experiments, and with two new tools in hand, Georg Ohm used the thermocouple and a galvanometer to quantitatively determine the relationship between the torque on the galvanometer and the length of a connecting wire. The following equation is the result of Ohm’s experiment.

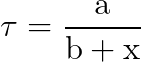
The torque, τ, on the galvanometer was directly proportional to a constant (a) determined by the temperature difference and inversely proportional to the total of the resistance of the circuit (b) and the wire (x)^[4]

This is not the equation normally attributed to Ohm. Ohm did not invent the Ohm’s Law we know today – he found a quantitative relationship between the temperature differential of a thermocouple, the length of wire, some constant in his system, and the torque on a galvanometer.

In his text on “Teaching Introductory Physics”, Arnold Arons notes that Ohm kept the diameter of the wire as a constant and experimented with different metals, noting that “the equation fits experiment very accurately nearly up to the extinction of the force by the resistance of the conductors.” In other words, there is no minimum potential difference needed to overcome resistance in a conductor. This is a very important finding^[5].

Ohm’s Law was likely developed without any knowledge of Cavendish’s work. But it didn’t become Ohm’s Law for several more years. In the next article we’ll take a look at James Prescott Joule’s discovery of Joule Heating.